Research

The Vicsek model (VM) describes flocking of animals and it is a paradigm of dry active matter. Examples include insect swarms, bird flocks, fish schools, etc. The model consists of N particles moving in a two or three dimensional space with constant speed. Particle positions and velocities are updated at discrete times. At a given discrete time, the velocity of each particle is directed along the average velocity of the particles in its metric or topological neighborhood plus an alignment noise. There are many numerical simulations of the VM with periodic boundary conditions and approximate descriptions thereof by means of kinetic theory and hydrodynamic equations. They have established that there is an unpolarized gas phase at large alignment noise that undergoes a continuous transition to an ordered liquid phase with constant polarization at a critical noise value. This phase is unstable at small wave numbers (that are active for sufficiently large sizes of the periodic box) and a number of stable moving bands and crossbands may coexist until the noise drops before a second critical value. Below this value, the liquid phase becomes stable. We have illustrated this scenario using bifurcation theory for a Enskog type kinetic theory proposed by Ihle. Changing the alignment rule so that each particle has a probability of following the majority as previously described or a contrarian rule, we have shown that the VM displays exotic phases with time periodic polarization.

Much more interesting phenomena occur if the particles are confined by a harmonic potential instead of an artificial periodic box. Numerical simulations of the 3D VM show that periodic, quasiperiodic and chaotic phases exist depending on the alignment noise, the confinement constant and the particle number. We have discovered a new phase transition with an extended critical region comprising different lines that collapse simultaneously to zero confinement parameter for infinite N. At finite N, these lines separate nonchaotic from chaotic phases and different chaotic phases among themselves (e.g., single-cluster chaotic phases comprising a condensed nucleus of particles and surrounded by a vapor of particles entering and leaving it are separated from polarized multicluster phases). The correlation length is proportional to the cluster size, which indicates scale free behavior. Using the finite size scaling hypothesis, we have found critical exponents for the correlation time, correlation length, susceptibility and the largest Lyapunov exponent. The mean field approximation produces the same static critical exponents as the Landau theory of equilibrium phase transitions. Moreover, we have discovered another phase transition at increasingly large confinements to infinitely dense clusters of finite size, which we have called flocking black holes. In our work, we have used and refined a variety of tools from dynamical systems, topological data analysis and statistical mechanics. Midges (small flies) enclosed in a large crystal box are known to form a swarm comprising a condensed nucleus and a vapor phase (Ouellette and collaborators). Observations of natural swarms by Cavagna and collaborators have provided static and dynamic critical exponents that are very close to our predictions. A mixture of data from the extended criticality region of our scale-free-chaos phase transition mimics observations obtained under different atmospheric conditions and different midge species.

https://doi.org/10.1103/PhysRevE.109.014611

https://doi.org/10.3390/e25121644

https://doi.org/10.1103/PhysRevE.107.L062601

https://doi.org/10.1103/PhysRevE.107.014209

https://doi.org/10.1103/PhysRevE.98.062603
https://doi.org/10.1103/PhysRevE.99.012612

Collective motion of epithelial cells

Confluent motion of epithelial cell monolayers is crucial in biological processes such as morphogenesis, pattern formation, aggregation and swarming, tissue repair, development, tumor invasion and metastasis. It is a simple paradigm for collective motion of cells that retain their cell-cell junctions as they move on a 2D substrate, and it can be tracked and visualized in experiments. Active vertex models consider cells as non-overlapping polygons in an irregular Voronoi tesselation of the plane whose centers are subject to forces of different origin. Some forces maintain tessellation and optimize the area and perimeter, others are inertial forces of biological origin, and there are active forces aligning the speeds of neighboring cells, as well as friction and noise. We have used SAMoS software to study formation of fingers in wound healing and encroaching of cancerous cells on healthy tissue. Topological data analysis allows to automatically group, plot and classify changes in the interfaces between tissues the cancer cells progress. We have also analyzed finger formation using a simple hydrodynamic model. We have also derived continuum models to study shear flow and induced cell asymmetry on supracellular length scales.

https://doi.org/10.1103/PhysRevE.108.044118

https://doi.org/10.1371/journal.pcbi.1008407
https://arxiv.org/abs/2009.14161
https://doi.org/10.1039/D1SM00626F
https://arxiv.org/abs/2104.05699

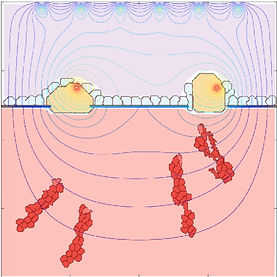
Modeling angiogenesis

Angiogenesis is a multiscale process by which blood vessels grow from existing ones and carry oxygen to distant organs. Angiogenesis is essential for normal organ growth and wounded tissue repair but it may also be induced by tumors to amplify their own growth. Mathematical and computational models contribute to understanding angiogenesis and developing anti-angiogenic drugs, but most work only involves numerical simulations and analysis has lagged. A recent stochastic model of the early stages of tumor induced angiogenesis including branching, elongation, and anastomosis (fusion) of blood vessels captures some of its intrinsic multiscale structures. Vessel tips proliferate due to branching, elongate following Langevin dynamics and, when they meet other vessels, join them by anastomosis and stop moving. Stalk endothelial cells follow the tip cells, so that the trajectories thereof constitute the advancing blood vessel. We have been able to extract a deterministic integropartial differential description of the vessel tip density that includes vessel proliferation and anastomosis for the first time. Anastomosis keeps the number of vessel tips relatively small, so that we cannot use the law of large numbers to derive equations for their density. Nevertheless, we show that ensemble averages over many replicas of the stochastic process correspond to the solution of the deterministic equations with appropriate boundary conditions. Most of the time, the density of tips sprouting from a primary blood vessel advances chemotactically towards the tumor driven by a soliton similar to the famous Korteweg-de Vries soliton. There are two collective coordinates whose slow dynamics changes the shape and velocity of the soliton. Higher moments of the density are also functionals of the soliton. Other models of leader-follower behavior also exhibit the same soliton. Analyzing the equations for the collective coordinates paves the way for controlling angiogenesis through the soliton, the engine that drives this process. We are working to extend our results to more realistic models using our results for the simpler model as a template for future research.

https://doi.org/10.1103/PhysRevE.108.054407

https://doi.org/10.1007/s00332-023-10006-2

https://doi.org/10.1088/1742-5468/aba598
https://doi.org/10.1016/j.jcp.2018.09.008
https://doi.org/10.1103/PhysRevE.94.062415
https://doi.org/10.1038/srep31296
https://doi.org/10.1103/PhysRevE.93.022413
https://arxiv.org/abs/1602.06937
https://doi.org/10.1103/PhysRevE.90.062716

Angiogenesis at the cellular scale

Understanding angiogenesis at the subcellular and cellular scale requires detailed computational models. We have developed a mathematical model of early stage angiogenesis that permits exploration of the relative importance of mechanical, chemical and cellular cues. Endothelial cells proliferate and move over an extracellular matrix by following external gradients of Vessel Endothelial Growth Factor (VEGF), adhesion and stiffness, which are incorporated to a Cellular Potts model with a finite element description of elasticity. The dynamics of Notch signaling involving Delta-4 and Jagged-1 ligands determines tip cell selection and vessel branching. Through their production rates, competing Jagged-Notch and Delta-Notch dynamics determine the influence of lateral inhibition and lateral induction on the selection of cellular phenotypes, branching of blood vessels, anastomosis (fusion of blood vessels) and angiogenesis velocity. Anastomosis may be favored or impeded depending on the mechanical configuration of strain vectors in the ECM near tip cells. Numerical simulations demonstrate that increasing Jagged production results in pathological vasculatures with thinner and more abundant vessels, which can be compensated by augmenting the production of Delta ligands. Current work involves incorporating the formation of lumen about newly formed vessels, blood perfusion and pruning of redundant vessels to the model.

https://doi.org/10.1371/journal.pcbi.1006919

Modeling age-related macular degeneration in the retina

Age-related macular degeneration (AMD) is a degenerative disease of the macula, the central area of the retina. There is currently no cure for the disease and it is characterized by a gradual loss of central vision and is the leading cause of blindness in developed countries in people over the age of 65. It is estimated that around 196 million people are affected worldwide and that this number will reach 288 million by 2040. There are two types of AMD: the dry or atrophic phase, which is usually the first and most common phase which progresses slowly; the acute phase, known as the wet or exudative phase, which occurs less frequently but has a worse prognosis at a visual level. In this latter form of AMD, there is an angiogenesis under the retina, an abnormal growth of very fragile blood vessels that may lose fluid or bleed, which can knock off and destroy the photoreceptor cells needed to see. With age, the Bruch membrane that separates the capillary vessels from the inner part of the retina becomes less permeable and, therefore, does not deliver enough oxygen or nutrients to the photoreceptors. They then emit VEGF that diffuses, passes to the blood vessels, and triggers angiogenesis, thereby causing wet AMD. We have used our Cellular Potts model of angiogenesis and a simple model of a deteriorated Bruch membrane to describe the disease. Numerical simulations of the model suggest that therapies based on decreasing growth factors and proteins that are crucial in angiogenesis may temporarily slow the disease down, while other therapies based on improving cell adhesion may be more effective in the long term. In addition to this, this model could be used to research other retinal diseases, such as diabetic retinopathy or that associated with premature babies, as, in these cases, these diseases also occur due to abnormal blood vessel growth.

https://doi.org/10.3390/biomedicines9020224
https://arxiv.org/abs/2104.00644

Spatially discrete models of protein unfolding

We have proposed and studied spatially discrete models of modular proteins, nucleic acids, and other biomolecules made out of several single units or modules. At a mesoscopic level of description, the configuration of the system is given by the elongations of each of the units. The system free energy includes a double-well potential for each unit and an elastic nearest neighbor interaction between them. Minimizing the free energy yields the system equilibrium properties whereas its dynamics is given by (overdamped) Langevin equations for the elongations, in which friction and noise amplitude are related by the fluctuation-dissipation theorem. Multistability of equilibrium extensions provides the characteristic sawtooth force-extension curve. We show that abrupt or stepwise unfolding and refolding under force-clamp conditions involve transitions through virtual states (which are quasi-stationary domain configurations) modified by thermal noise. These predictions agree with experimental observations. Our models and results are structurally related to models of nonlinear electron transport in semiconductor superlattices and dislocations in solids that we proposed in the past.

https://doi.org/10.1103/PhysRevE.91.052712
https://arxiv.org/abs/1410.3885
https://doi.org/10.1209/0295-5075/108/28002
https://arxiv.org/abs/1409.7900

Defects and ripples in graphene

We have studied the stability and evolution of various elastic defects in a flat graphene sheet and the electronic properties of the most stable configurations. Our stability studies use elementary periodized discrete elasticity models of graphene sheets. Two types of dislocations are found to be stable: 'glide' dislocations consisting of heptagon–pentagon pairs, and 'shuffle' dislocations, an octagon with a dangling bond. Unlike the most studied case of carbon nanotubes, Stone Wales defects seem to be dynamically unstable in the planar graphene sheet. This fact has recently been corroborated by experimental observations. Similar defects in which one of the pentagon–heptagon pairs is displaced vertically with respect to the other one are found to be dynamically stable. Shuffle dislocations will give rise to local magnetic moments that can provide an alternative route to magnetism in graphene. In a suspended graphene sheet, we have included bending effects and the possibility that the sheet be locally curved upwards or downwards. We find a critical temperature above which a flat sheet is stable and below which stable ripples appear. Rippling in the presence of defects is also being studied.

https://doi.org/10.1126/science.1224681
https://doi.org/10.1103/PhysRevB.92.155417
https://arxiv.org/abs/1510.00307
https://doi.org/10.1007/s00161-011-0182-0
https://arxiv.org/abs/1101.5818
https://doi.org/10.1103/PhysRevB.86.195402
https://arxiv.org/abs/1211.0527
https://doi.org/10.1088/1742-5468/2012/09/P09015
https://arxiv.org/abs/1211.0541
https://doi.org/10.1103/PhysRevB.94.205404
https://arxiv.org/abs/1610.05222

Rippling phase transition in graphene

We have proposed a model for the formation of ripples in suspended graphene membranes. It consists of a tight binding Hamiltonian for Dirac electrons coupled to the classical energy of the membrane. At zero absolute temperature, we find that the critical value of the coupling rapidly decays as the system increases its size, in agreement with the experimental observation of an unavoidable stable rippled state for suspended graphene membranes. This decay turns out to be controlled by a power law with a critical exponent ∼1/2. Consistent arguments based on bifurcation theory indicate that the phase transition is discontinuous at large scaling parameter k, that the jump in the order parameter decreases as the reciprocal square root of k, and that the phase transition becomes continuous at infinite size, with a critical exponent 1/4 for the order parameter scaling. We are extending the theory to finite temperatures. The critical coupling decreases with temperature and the susceptibility of the rippling phase transition (at infinite size) has a critical exponent 1/4.

https://doi.org/10.1103/PhysRevB.101.235428
https://arxiv.org/abs/1911.10510
https://doi.org/10.1103/PhysRevB.93.115407
https://arxiv.org/abs/1603.03961

Fluctuation-induced current and charging effects in freestanding graphene

At room temperature, micron-sized sheets of freestanding graphene are in constant motion, even in the presence of an applied bias voltage. We quantify the out-of-plane movement by collecting the displacement current using a nearby small-area metal electrode and present an Ito-Langevin model for the motion coupled to a circuit containing diodes. Numerical simulations show that the system reaches thermal equilibrium and the average rates of heat and work provided by stochastic thermodynamics tend quickly to zero. However, there is power dissipated by the load resistor, and its time average is exactly equal to the power supplied by the thermal bath. The exact power formula is similar to Nyquist’s noise power formula, except that the rate of change of diode resistance significantly boosts the output power, and the movement of the graphene shifts the power spectrum to lower frequencies. We have calculated the equilibrium average of the power by asymptotic and numerical methods. Excellent agreement is found between experiment and theory. This is a collaboration with the group of P. Thibado (University of Arkansas). It is possible to charge additional capacitors for sufficiently long times before thermal equilibrium with the bath settles down. Ongoing work shows how to charge additional capacitors and continuously harvest energy from fluctuations by keeping the two diodes in the circuit at different temperatures.

https://doi.org/10.1103/PhysRevE.108.024130

https://doi.org/10.1103/PhysRevE.102.042101

Multiscale methods

Studying the impact of defects in the macroscopic properties of a solid material is a multiscale problem that involves processes taking place at scales ranging from the atomic scale to the macroscale. Finding a way to transfer the relevant information from the lower scales to the upper scales is a largely unsolved problem. A basic problem in this context consists in developing hybrid schemes that couple an atomistic description in a localized region with a continuum description around it. Discretizing the surrounding continuum by means of finite element schemes may give rise to singularities and reflections by an abrupt change in the mesh. We are exploring different ways to couple the atomistic and the continuum region: nonreflecting coupling conditions based on discrete Green functions, perfectly matched layers, meshless methods...

Nonlinear transport in nanostructures

Nonlinear charge and spin transport in nanostructures is essential to propose and model electronic and spintronic devices and yet there are fundamental issues that are poorly understood. We derive quantum and semiclassical kinetic equations describing charge and spin transport in simple nanostructures (semiconductor superlattices and lateral superlattices) in order to obtain and solve reduced equations for electron densities and electric field and compare and validate the results obtained using these different descriptions. Recently, we have used efficient data processing tools to uncover spatiotemporal patterns in semiconductor superlattices.

https://www.wiley.com/en-us/Nonlinear+Wave+Methods+for+Charge+Transport-p-9783527628681 https://doi.org/10.1088/0034-4885/68/3/R03

https://doi.org/10.1103/PhysRevE.104.035303
https://arxiv.org/abs/2109.14660
https://doi.org/10.1103/PhysRevE.96.062215
https://arxiv.org/abs/1712.04559
https://doi.org/10.1103/PhysRevB.90.165441
https://arxiv.org/abs/2109.14660
https://doi.org/10.1016/j.jcp.2012.02.024
https://arxiv.org/abs/1205.1292
https://doi.org/10.1103/PhysRevB.84.155316
https://arxiv.org/abs/1109.6857

Spontaneous chaos at room temperature and true random number generators

Recently, spontaneous chaos at room temperature has been discovered in semiconductor superlattices, which opens the possibility to build fast true random number generators to use in secure communications, encryption, etc. The source of entropy producing true random numbers is quantum tunneling through quantum barriers separating quantum wells in the superlattice. This randomness is enhanced by chaotic attractors at the mesoscopic level. In the lab, these superlattice devices have been shown to produce bit rates up to 80Gbits per second, way above the usual generators that produce 1Gb/s. We have proposed and analyzed models for charge transport in weakly coupled semiconductor superlattices that explain different possible types of spontaneous chaos at room temperature depending on the device configuration, randomness in doping density and configuration, and thermal and shot noise. We have also proposed a modification of the superlattice configuration, adding two identical quantum wells that are wider than the others. In this configuration, we have found by numerical simulations of the model hyperchaos and intermittent chaos. These configurations have faster and more robust chaotic attractors and can be achieved with state of the art epitaxial growth techniques.

https://doi.org/10.1103/PhysRevLett.127.0496601

https://arxiv.org/abs/2108.11843
https://doi.org/10.3390/e24121702
https://arxiv.org/abs/2211.15250

Coherence resonance and stochastic resonance in semiconductor superlattices

Adding appropriate external noise, we can drive a semiconductor superlattice device from a stationary state to a self-sustained oscillation of the current, which is called coherence resonance. The results of numerical simulations have been demonstrated in the laboratory through a collaboration with the groups of Y. H. Zhang (SINANO, Chinese Academy of Sciences) and H. T. Grahn (Paul Drude Institute for Solid State Electronics, Berlin). This effect allows detection of very weak ac external voltage signals when they become locked to the oscillation mode of the coherence resonance via stochastic resonance. It can be used to detect signals that are hidden in large amounts of noise or, inversely, to cypher signals by embedding them in noisy backgrounds and recovering them later. Examples include extracting a recorded conversation from a loud room, astronomical observations with large background, image processing, and so on.

https://doi.org/10.1103/PhysRevLett.121.086805
https://doi.org/10.1103/PhysRevLett.121.086806
https://arxiv.org/abs/2011.09327

Protein

Graphene_def

Phase_graphene

Fluctuations_graphene

Multiscale

Nonlinear

Spontaneous_chaos

Coherent_resonance